First, a direct optimization with a Multi Objective Genetic Algorithm (namely, NSGA-II) allowed the designer to explore the wide range of possible solutions. For some reasons, the results were not fully satisfactory: namely, the comfort (target objective) has been over-optimized respect to the heat loss. For time constraint reasons, only a few extra computations were still available, so an advanced strategy was set up. The proposed approach is aimed to quickly reach a desired zone of the Pareto Set that was not mapped by the initial optimization. First an application of SOM techniques has been used to detect local correlations, and hence to circumscribe the scope of the search in the input variables’ space, “reducing” the problem. After the definition of new bounds for the input variables, a new Design of Experiment (DOE) campaign was set up and evaluated through CFD model runs, and the new data has then been interpolated with Response Surface Modeling (RSM) techniques. Finally, an almost instantaneous run of the Genetic Algorithm has been applied to these meta-models, and the most promising forecasts were validated by means of new CFD simulations, delivering the final result to the designer.

Apart from the improvements obtained with regard to the initial design, this kind of hybrid methods guarantee a reduction of the computational efforts needed to obtain such results, compared to a full direct optimization. In particular, the usage of SOM techniques allows the designer to select the most promising area for the objectives of his search. This technology brings two major advantages to such kind of applications. First, it becomes even more time-saving and convenient with regard to other approaches while the dimension of the input variables’ space increases. Secondly, the process of bounds focusing takes advantage not only of the computed solutions, but also of the estimation of the probability density of the solution space.

Initially, the bounds of the 10 independent input variables were quite wide, in order to map the space of the possible solutions in an exhaustive way. With such setup, a multi-objective NSGA- II algorithm has been used to drive the CFD code in exploring new designs.
The initial population of 20 designs has been obtained adding a Random DOE (Design Of Experiments) sequence to the original design. The genetic algorithm has been run for 15 generations, with a crossover probability of 0.9 and a mutation probability of 1.0. All constraints have been considered as penalty functions for the assigned objectives.
Figure 3 shows the evolution of the target objective value during the optimization. Figure 4 depicts the scatter chart of the explored configurations in the two objectives (target and heat loss) plane. In this first phase of the optimization, the algorithm was able to exit the unfeasible region it started from (the initial population could not achieve the assigned constraint on target).

Figure 4 highlights also that the algorithm focused on two main regions of feasible solutions, and tended to over - optimize the values of humidity and temperature, while the heat loss was not improved sufficiently. In fact, the cloud of feasible points at the bottom of figure 4 has still an appreciable margin from the limit assigned to the deviation from the ideal climate control performance (target less than 0.025).
Since target and heat loss seem to be opposing goals, it can be expected to find some configurations able to improve further the heat loss by staying more tight to the constraint assigned to target. The idea is to search for them in the most efficient way, exploiting the data already available after the optimization step with NSGA-II, plus few other well-targeted CFD simulations.
To this purpose, a virtual optimization applying a hybrid SOM-RSM strategy is proposed here. An advantage of this approach compared to a longer direct optimization (apart from the reduced number of additional simulations needed to find the desired solutions) is a more thorough understanding of the local correlations between parameters and optimization goals. This becomes even more clear when increasing the number of variables and responses involved.

The Self-Organizing Map (SOM) is an algorithm that projects high dimensional data onto a two-dimensional map. The projection preserves the topology of the data so that similar data items will be mapped to nearby locations on the map.</>

In the proposed approach, the SOM has been used to analyze local correlations between the two objectives (target and heat loss index) exploiting the results of the previous NSGA-II optimization.
In fact, detecting such local correlations allows to identify a reduced input parameter range that includes the most promising designs for the desired output values. In this way, a subsequent search campaign could be set up within this reduced input parameter space.

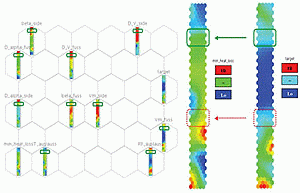
Figure 5 displays the component charts relative to the built SOM. The grid on the left collects the whole set of SOM component charts, and in particular also the design parameters. At the right, the component charts of target and heat loss index are shown in detail. In such conventional charts, each hexagon is a “box” containing a group of similar designs, previously computed by the CFD model or interpolated by the SOM’s unsupervised neural network. They are “similar” with respect to the complete vector of parameters and output values, which define them in the n-dimensional space. Adjacent hexagons mean similar groups. A corresponding hexagon in 2 different parameter’s maps (i.e. an input and an output one) represents the same “box”, hence including the same set of designs. The hexagon’s color, conversely, depends on the map itself: it represents the averaged value of such parameter within the selected group of designs included in the “box”. Comparing the color pattern of a corresponding set of hexagons in two different maps, means looking for a set of designs with a certain common trend of parameters (local correlation between the parameters).

Therefore, local correlations between a couple of parameters can be detected comparing their SOM maps and searching for zones where hexagons have similar color patterns. Since the goal here is to check whether a local correlation exists between the heat loss and a target value slightly less than 0.025, their SOM charts are compared in Figure 5 (right). A local correlation of the two outputs, where target is a bit lower than 0.025 (pale blue color), exists in the SOM units underlined with a solid line in Figure 5 top-right, as the similar uniform color pattern testifies. As an example, no local correlation can be assessed for the design groups in the dotted line square, (Figure 5 bottom-right): the corresponding target and heat loss color patterns are not similar.

After selecting the hexagons included in the solid line box in the right side of Fig.5, a re-definition of the design space has been achieved by restricting the design parameter to the range defined by the designs included in such SOM units (represented by the range of colors of the corresponding hexagons in the left side of Fig.5, the green-framed ones). Each one of the input variable ranges has been reduced sensibly, in most of the cases more than halved, with an average reduction of 43%: this means that the size of the search domain is strongly reduced and focused only to the most promising zones with regards to the designer’s requirements. This leads to a much faster second step optimization. A Reduced Factorial DOE sequence of 16 configurations has been set up, in order to add uniformly few new points in such restricted input parameter space. All the previously simulated designs belonging to the selected SOM units, and hence falling within the restricted range, were added to the Reduced Factorial DOE result database. Then a RSM, namely a set of Radial Basis Functions (RBF), were trained with that data, in order to model each of the problem’s goals. Such RSMs have then been used to interpolate new configurations, disconnecting the link between the optimizer and the computationally expensive CFD calculations. In fact, upon such RSMs, a new extensive NSGA-II optimization has been performed in order to search for optimum(s) with reduced heat loss values, respecting the constraint target. In this way, approximately 1800 points were estimated in a few seconds. The results have then been filtered according to the dominance criteria, and the most promising design candidates were selected to be validated with new CFD simulations. This choice was done taking into account not only the estimated values of the goals, but also the distance of such points with respect to the training set points in the 10-dimensional parameter space. Three designs have been selected and subsequently validated with new CFD simulations.